The Julian Date Calendar and the Leap Year Conundrum: A Deep Dive

Related Articles: The Julian Date Calendar and the Leap Year Conundrum: A Deep Dive

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Julian Date Calendar and the Leap Year Conundrum: A Deep Dive. Let’s weave interesting information and offer fresh perspectives to the readers.

The Julian Date Calendar and the Leap Year Conundrum: A Deep Dive

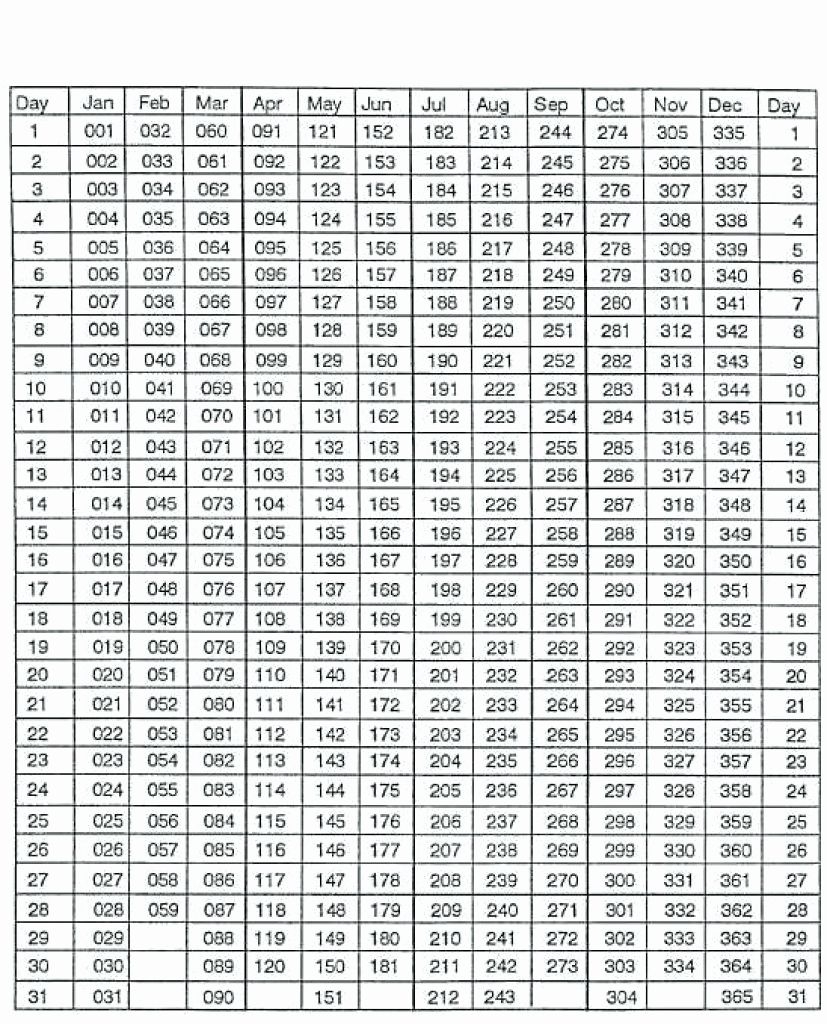
The Julian date calendar, a system for assigning a unique number to each day, offers a remarkably simple and elegant way to track time. Unlike the Gregorian calendar we commonly use, which is based on cyclical years with varying lengths, the Julian date system provides a continuous count of days, eliminating the complexities of months and their irregular lengths. This simplicity, however, doesn’t entirely eliminate the need to account for leap years, a necessary adjustment to align the calendar with the Earth’s actual orbital period. This article delves into the intricacies of leap years within the context of the Julian date system, exploring their calculation, their significance, and their subtle differences compared to the Gregorian calendar’s leap year rules.

Understanding the Julian Date System:

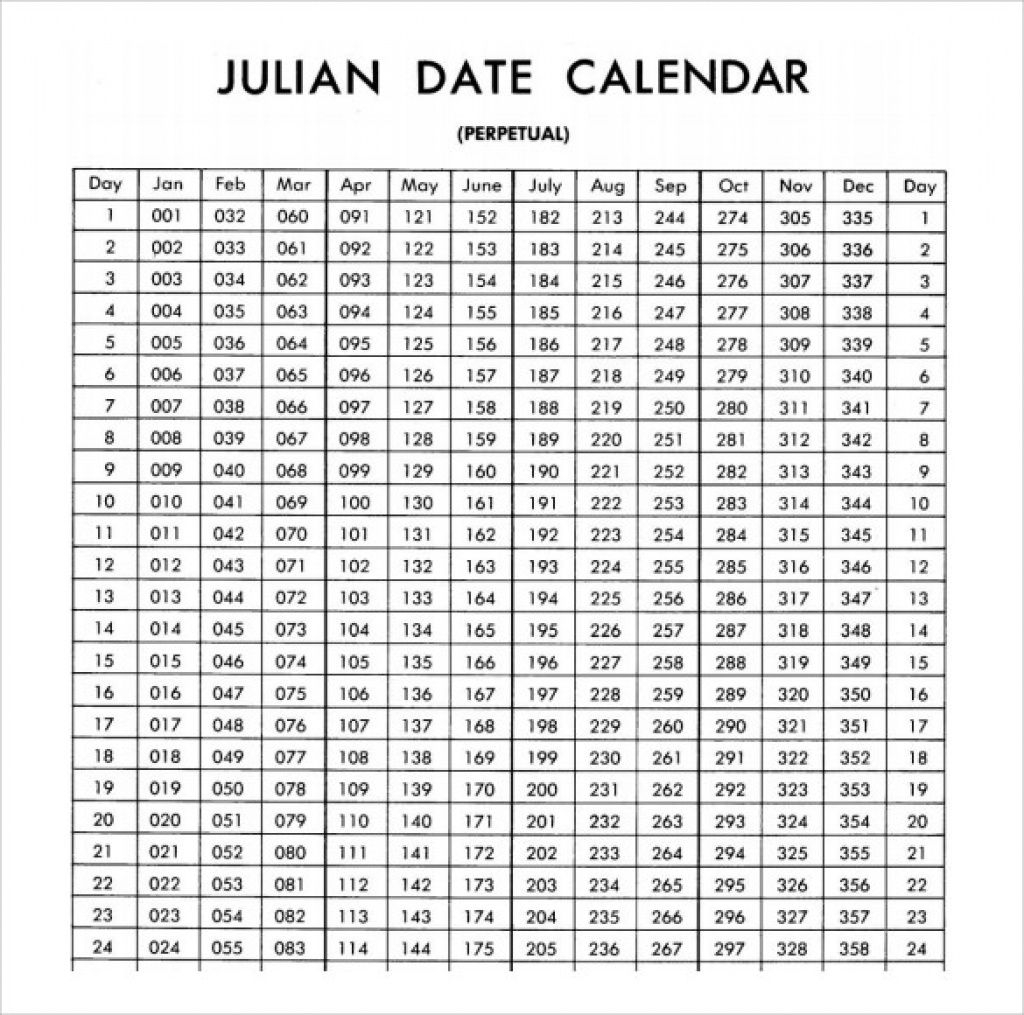
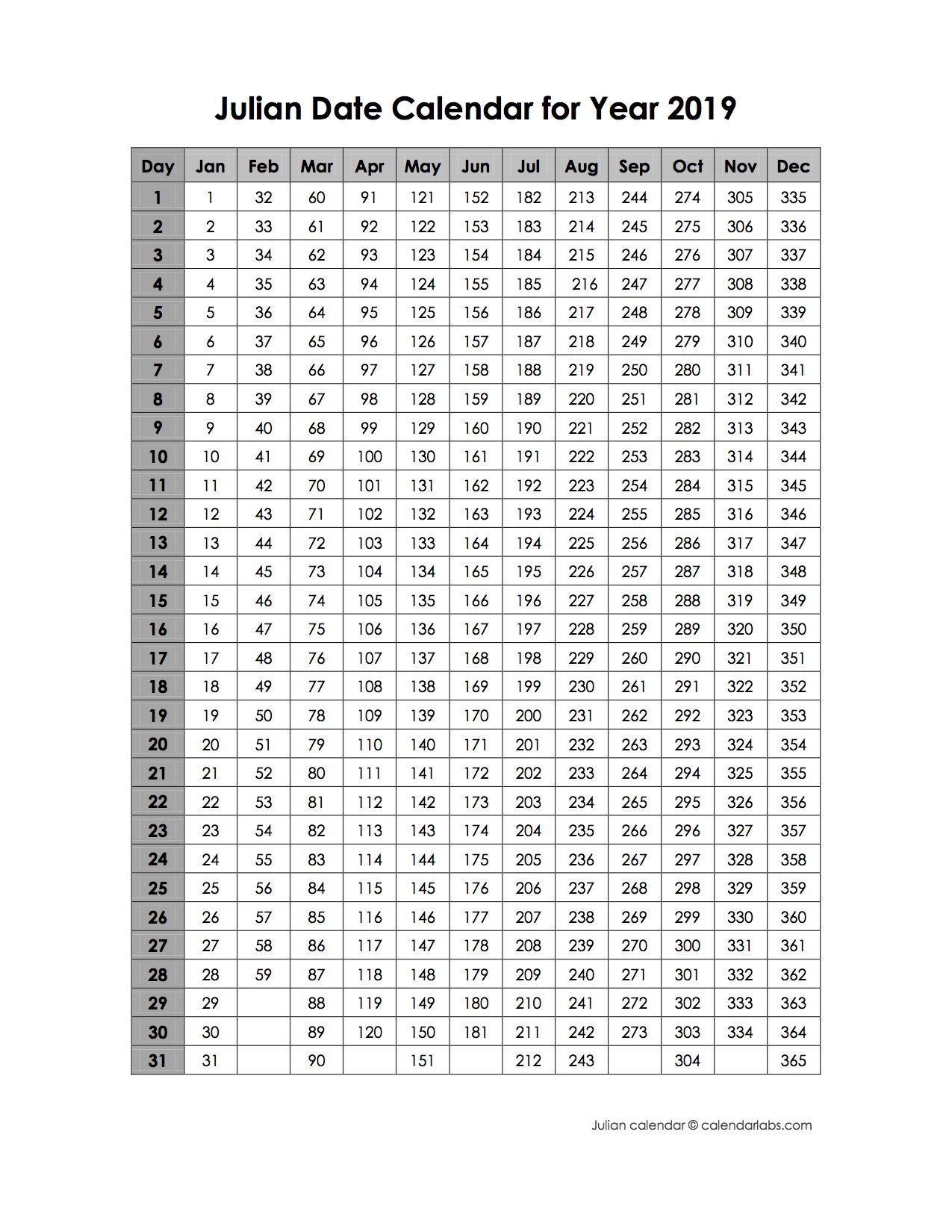
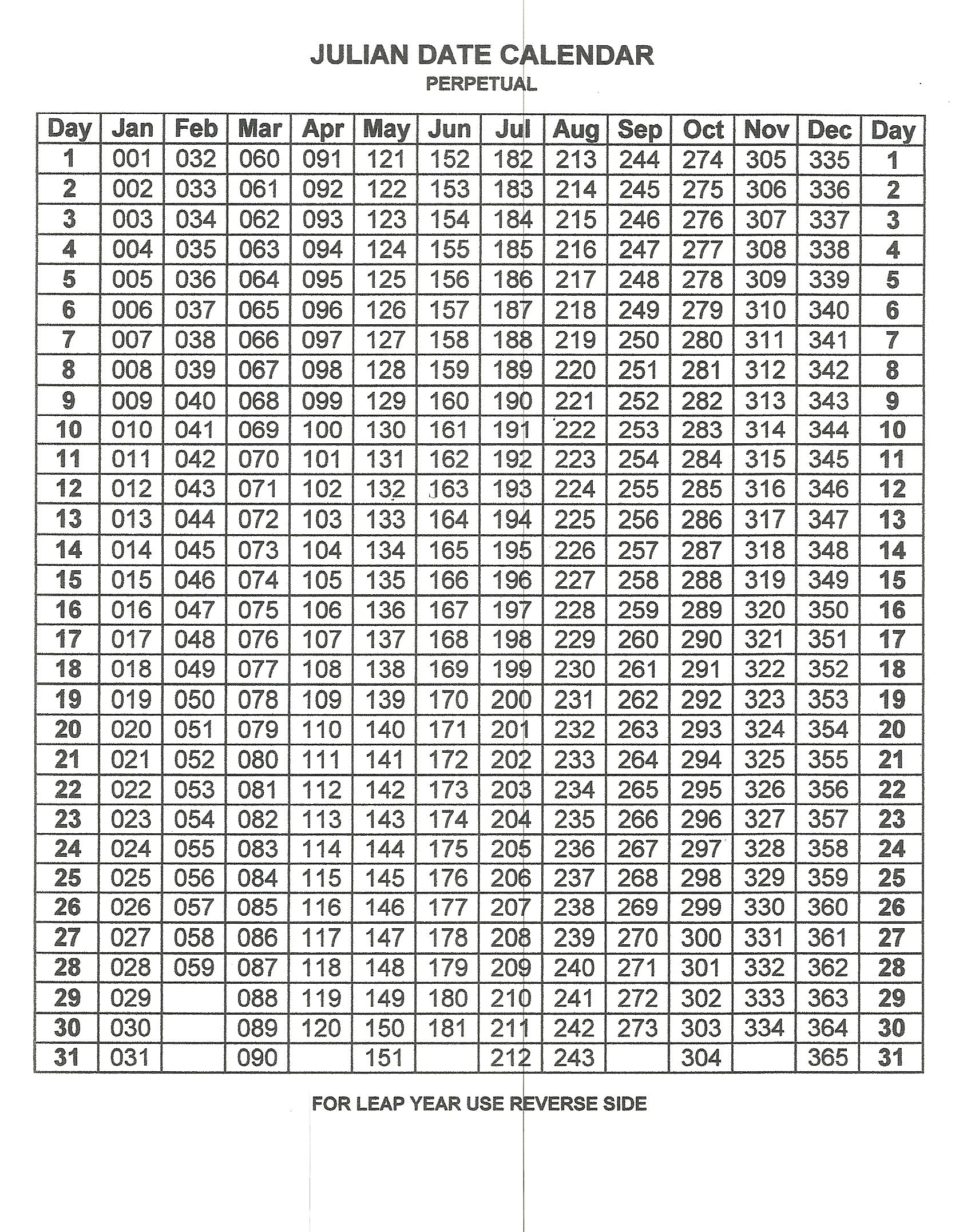
Before diving into leap years, it’s crucial to grasp the fundamental principles of the Julian date system. The system is based on a continuous count of days since a specific epoch, conventionally chosen as January 1, 4713 BC, in the proleptic Julian calendar. Each day receives a unique number, irrespective of the month or year in the Gregorian calendar. This continuous numbering simplifies many calculations involving time spans, making it invaluable in astronomy, geodesy, and other fields requiring precise time tracking.

The Julian date (JD) is expressed as a fractional number. The integer part represents the number of days since the epoch, while the fractional part represents the fraction of a day elapsed since midnight. For example, JD 2458850.5 represents noon on January 1, 2020.

The Need for Leap Years in the Julian System:

The Earth’s orbital period around the sun isn’t exactly 365 days; it’s closer to 365.2422 days. This discrepancy, known as the tropical year, necessitates the addition of leap days to prevent the calendar from drifting out of sync with the seasons. The Julian calendar, initially devised by Julius Caesar, addressed this by adding a leap day every four years. This simple rule, while effective in its time, resulted in a slight overestimation of the tropical year.

Julian Leap Year Rule: A Simple but Imperfect Solution:

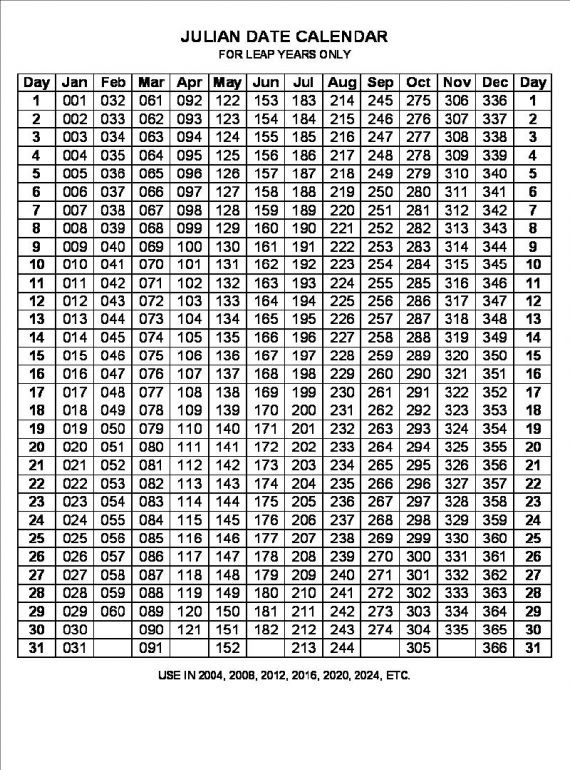
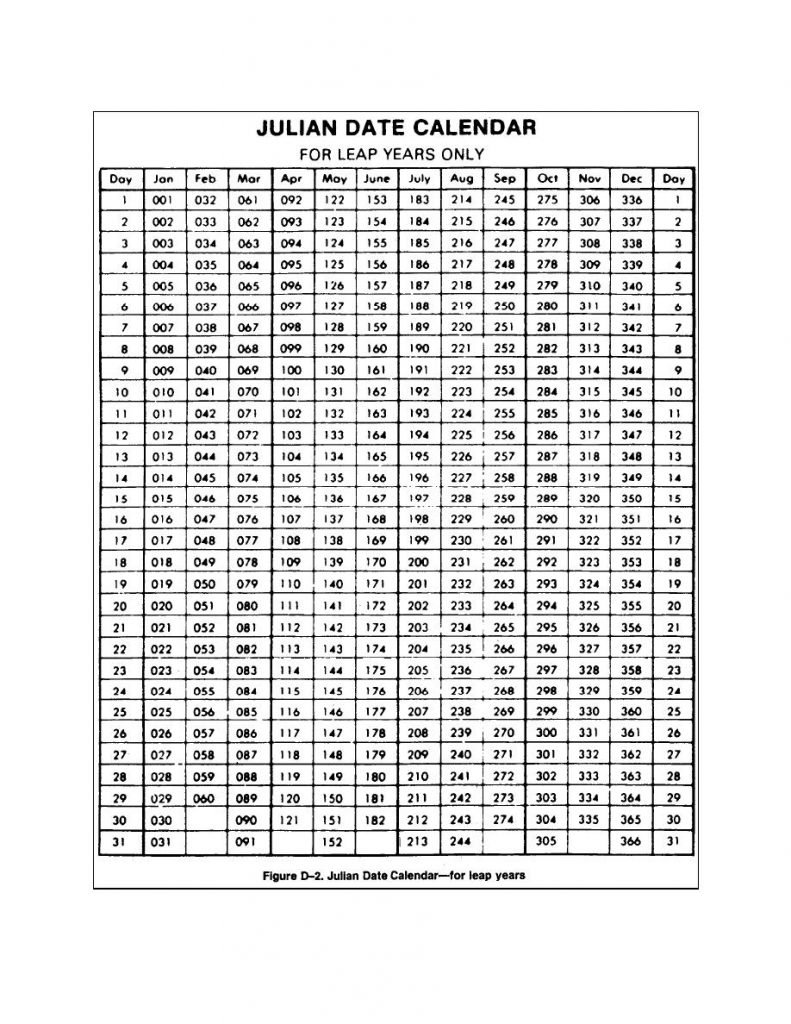
The fundamental rule for Julian leap years is straightforward: a year is a leap year if it’s divisible by four. This means years like 2000, 1996, and 2024 are considered leap years in the Julian system. However, this rule leads to an excess of approximately 11 minutes per year, accumulating to a significant error over centuries. This error is the primary reason why the Gregorian calendar, with its more refined leap year rules, eventually superseded the Julian calendar for civil use.

The Gregorian Calendar’s Refinement:

The Gregorian calendar, introduced in 1582, aimed to rectify the accumulated error of the Julian calendar. It retains the basic four-year cycle but introduces two additional rules:

1. Centennial years: Years divisible by 100 are not leap years unless they are also divisible by 400. This means that while 2000 was a leap year (divisible by 400), 1900, 1800, and 1700 were not.
2. Further Refinement: The Gregorian calendar is still slightly inaccurate, accumulating an error of approximately one day every 3,300 years. Future calendar reforms might be necessary to maintain long-term accuracy.

Julian Dates and the Implications of Leap Year Discrepancies:

The discrepancy between the Julian and Gregorian leap year rules has important implications when working with Julian dates. The continuous numbering of days in the Julian date system doesn’t inherently account for the Gregorian calendar’s more precise leap year rules. Converting between Julian dates and Gregorian dates requires careful consideration of these differences. Software and algorithms for such conversions must explicitly account for the Gregorian leap year exceptions to avoid errors.

Calculating Julian Dates Considering Leap Years:

Algorithms for calculating Julian dates usually incorporate a function to determine whether a given year is a leap year. For the Julian system, this is a simple check for divisibility by four. However, for conversion to and from Gregorian dates, the algorithm must incorporate the more complex Gregorian leap year rules. These algorithms often use modular arithmetic and conditional statements to accurately handle the leap year exceptions.

Practical Applications and Considerations:

The Julian date system’s simplicity makes it particularly useful in scientific and engineering applications where precise time tracking is critical. Astronomers, for example, frequently use Julian dates to record observation times, allowing for easy calculation of time intervals between events. Geodesists use Julian dates to timestamp geospatial data, ensuring accurate temporal referencing.

However, the discrepancy between the Julian and Gregorian calendars must always be considered when applying Julian dates in contexts involving civil dates. Converting between the two systems requires careful attention to the leap year differences, and using appropriate conversion algorithms is essential to avoid errors.

The Future of Leap Years and Calendar Reform:

The Gregorian calendar, while a significant improvement over the Julian system, is not perfectly accurate. The subtle error accumulating over millennia might necessitate future calendar reforms. Proposals for calendar reform often involve different approaches to handling leap years, aiming for even greater accuracy in aligning the calendar with the Earth’s orbital period. These proposals often involve more complex rules or longer cycles to minimize the accumulated error.

Conclusion:

The Julian date calendar, with its continuous day numbering, offers a powerful tool for precise timekeeping. However, its reliance on the simple Julian leap year rule introduces a degree of inaccuracy compared to the Gregorian calendar’s more refined approach. Understanding the differences between the Julian and Gregorian leap year rules is crucial for anyone working with Julian dates, particularly when converting between Julian dates and Gregorian dates. The ongoing quest for calendar accuracy highlights the enduring challenge of aligning our human-created systems with the complexities of the natural world. As our understanding of the Earth’s orbital mechanics improves, future refinements to the leap year rules may be necessary to maintain the long-term accuracy of our calendars, ensuring that our temporal frameworks remain aligned with the rhythms of our planet. The seemingly simple concept of the leap year, therefore, reveals a fascinating interplay between astronomical precision, calendrical convention, and the ongoing evolution of our methods for measuring time.

Closure

Thus, we hope this article has provided valuable insights into The Julian Date Calendar and the Leap Year Conundrum: A Deep Dive. We thank you for taking the time to read this article. See you in our next article!