From Julian Dates to Calendar Dates: A Comprehensive Guide

Related Articles: From Julian Dates to Calendar Dates: A Comprehensive Guide

Introduction

With great pleasure, we will explore the intriguing topic related to From Julian Dates to Calendar Dates: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

From Julian Dates to Calendar Dates: A Comprehensive Guide

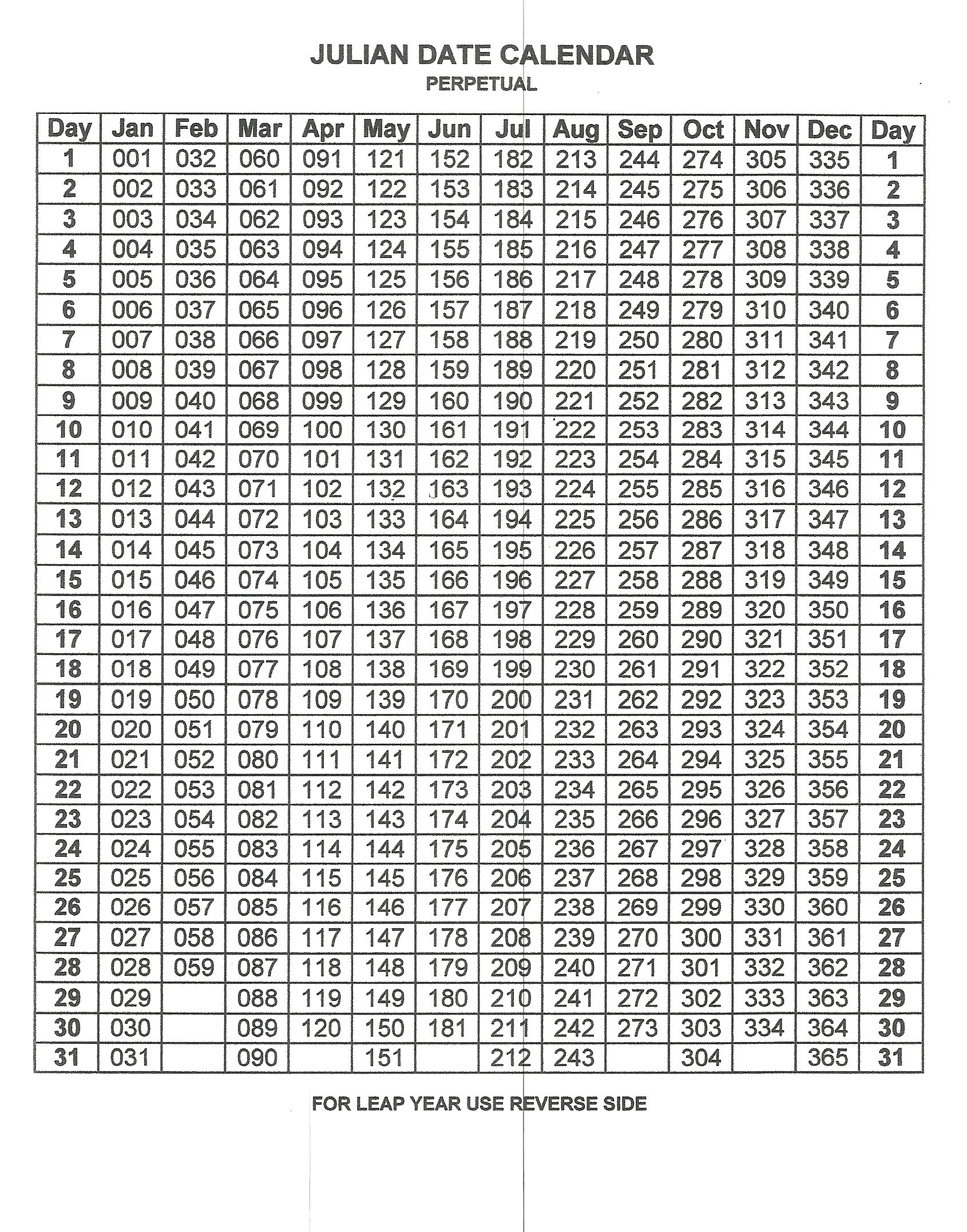
The Julian date system, a continuous count of days since a specific epoch, offers a concise and unambiguous way to represent dates. Unlike calendar dates, which are susceptible to variations based on the calendar system (Gregorian, Julian, etc.) and the complexities of leap years, Julian dates provide a consistent numerical representation. This makes them invaluable in scientific applications, particularly in astronomy, where precise timing is critical. However, converting a Julian date to a readily understandable calendar date requires a clear understanding of the underlying algorithms and the nuances of the Gregorian calendar. This article delves into the intricacies of this conversion, providing a detailed explanation of the process, the algorithms involved, and considerations for different programming languages.

Understanding Julian Dates

The Julian date (JD) is a continuous count of days since the beginning of the Julian period, which is conventionally set to noon Universal Time (UT) on January 1, 4713 BC in the proleptic Julian calendar. This choice of epoch provides a convenient reference point spanning a vast period of time, encompassing historical events and future projections. The number itself is a fractional value, with the fractional part representing the fraction of a day since noon. For instance, JD 2458850.5 represents noon UT on January 1, 2020.

The Importance of the Modified Julian Date (MJD)

While the Julian date is comprehensive, its large numerical values can be cumbersome. To address this, the Modified Julian Date (MJD) was introduced. The MJD is simply the Julian date minus 2,400,000.5. This offset reduces the magnitude of the numbers, simplifying calculations and storage. The epoch for the MJD is midnight UT on November 17, 1858.

Converting Julian Dates to Calendar Dates: The Algorithm

The conversion from a Julian date (or MJD) to a calendar date involves several steps. The fundamental approach relies on iterative algorithms that account for the irregularities of the Gregorian calendar, particularly leap years. Here’s a breakdown of the process:

1. Adjust for Modified Julian Date (if applicable): If you’re working with an MJD, add 2,400,000.5 to obtain the Julian date.

2. Determine the number of days since the epoch: This is simply the integer part of the Julian date.

3. Account for the Gregorian calendar reform: The Gregorian calendar was introduced in 1582, replacing the Julian calendar. The algorithm must account for the difference in the number of leap years between the two calendars.

4. Calculate the approximate year: A reasonable approximation can be obtained by dividing the number of days since the epoch by 365.25 (the average number of days in a year). This provides an estimate of the year.

5. Refine the year estimation: This approximation needs refinement to account for leap years accurately. An iterative process may be necessary to pinpoint the correct year. This involves comparing the calculated number of days with the actual number of days elapsed in the approximated year, considering leap years.

6. Calculate the day of the year: Once the year is determined, the day of the year can be calculated by subtracting the cumulative number of days in the preceding months.

7. Determine the month and day: With the day of the year known, the month and day can be determined by referencing a lookup table or using conditional statements based on the number of days in each month.

8. Handle leap years: The algorithm must explicitly handle leap years, ensuring that February 29th is correctly accounted for in leap years. Leap years occur every four years, except for years divisible by 100 but not by 400.

Example: Converting JD 2458850.5

Let’s convert JD 2458850.5 to a calendar date using a simplified algorithm (ignoring some finer details for brevity):

1. JD = 2458850.5 (This is already a Julian date, so no MJD adjustment is needed).

2. Days since epoch ≈ 2458850 (Integer part)

3. Approximate year ≈ 2020 (Days since epoch / 365.25)

4. Refine year: By checking the number of leap years and days in preceding years, we confirm that the year is indeed 2020.

5. Day of year: After accounting for the number of days in January and the preceding months, we find that this is the 1st day of the year.

6. Month and day: January 1st

7. Therefore, JD 2458850.5 corresponds to January 1, 2020, at noon UT.

Programming Language Implementations

The conversion algorithm can be implemented in various programming languages. Many libraries and packages provide built-in functions for this purpose. However, understanding the underlying principles allows for a more robust and adaptable solution.

Python Example:

Python’s datetime and calendar modules can be used to perform this conversion. However, a dedicated function is often more efficient and readable:

import datetime

def julian_to_calendar(jd):
  """Converts a Julian date to a calendar date."""
  jd = jd + 0.5  # Adjust for noon
  mjd = jd - 2400000.5
  a = int(mjd) + 68569
  n = int(4 * a / 146097)
  a = a - int((146097 * n + 3) / 4)
  b = int(8000 * a / 1461001)
  a = a - int(1461 * b / 4) + 31
  c = int(80 * a / 2447)
  d = int(c * 31 / 2448)
  e = int(2447 * c / 80)
  day = a - int(2447 * d / 80)
  year = int(4 * b + c / 11) - 4716
  month = int(c / 11)
  if month <= 2:
      year -= 1
  if month == 11:
      month = 11
  elif month == 12:
      month = 12
  else:
      month = month + 1

  return datetime.date(year, month, day)

jd = 2458850.5
calendar_date = julian_to_calendar(jd)
print(f"Julian Date jd corresponds to calendar_date")

Considerations and Limitations

• Accuracy: The accuracy of the conversion depends on the precision of the algorithm and the handling of leap years. For highly precise applications, more sophisticated algorithms might be necessary.
• Time Zone: Julian dates are typically referenced to Universal Time (UT). Conversions to local time zones require accounting for the time zone offset.
• Calendar System: The algorithms presented here primarily focus on the Gregorian calendar. For dates before the Gregorian calendar reform, adjustments are necessary to account for the Julian calendar.
• Fractional Days: The fractional part of the Julian date represents the fraction of a day. This needs to be considered when converting to a time component.

Conclusion

Converting Julian dates to calendar dates is a crucial task in many scientific and historical applications. Understanding the underlying algorithms and the intricacies of the Gregorian calendar is essential for accurate conversions. While pre-built libraries can simplify the process, a thorough understanding of the methodology enables developers to build robust and adaptable solutions for diverse applications. The examples provided offer a starting point for implementing these conversions in various programming languages, allowing for seamless integration into a wide range of projects requiring precise date handling. Remember to always consider the specific requirements of your application, particularly concerning accuracy and time zone considerations, when choosing and implementing a Julian-to-calendar date conversion algorithm.

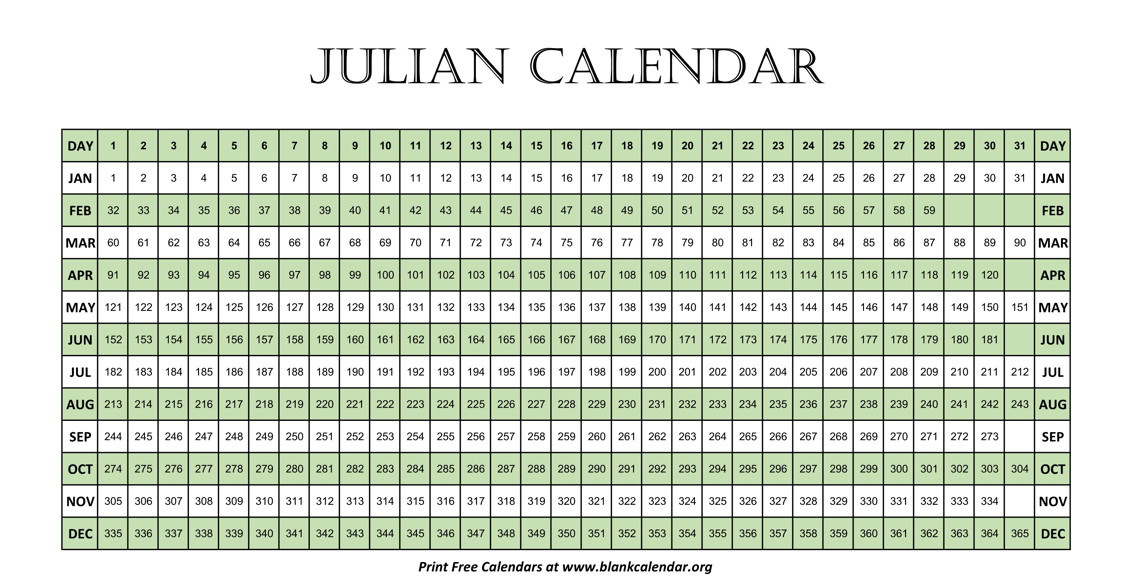
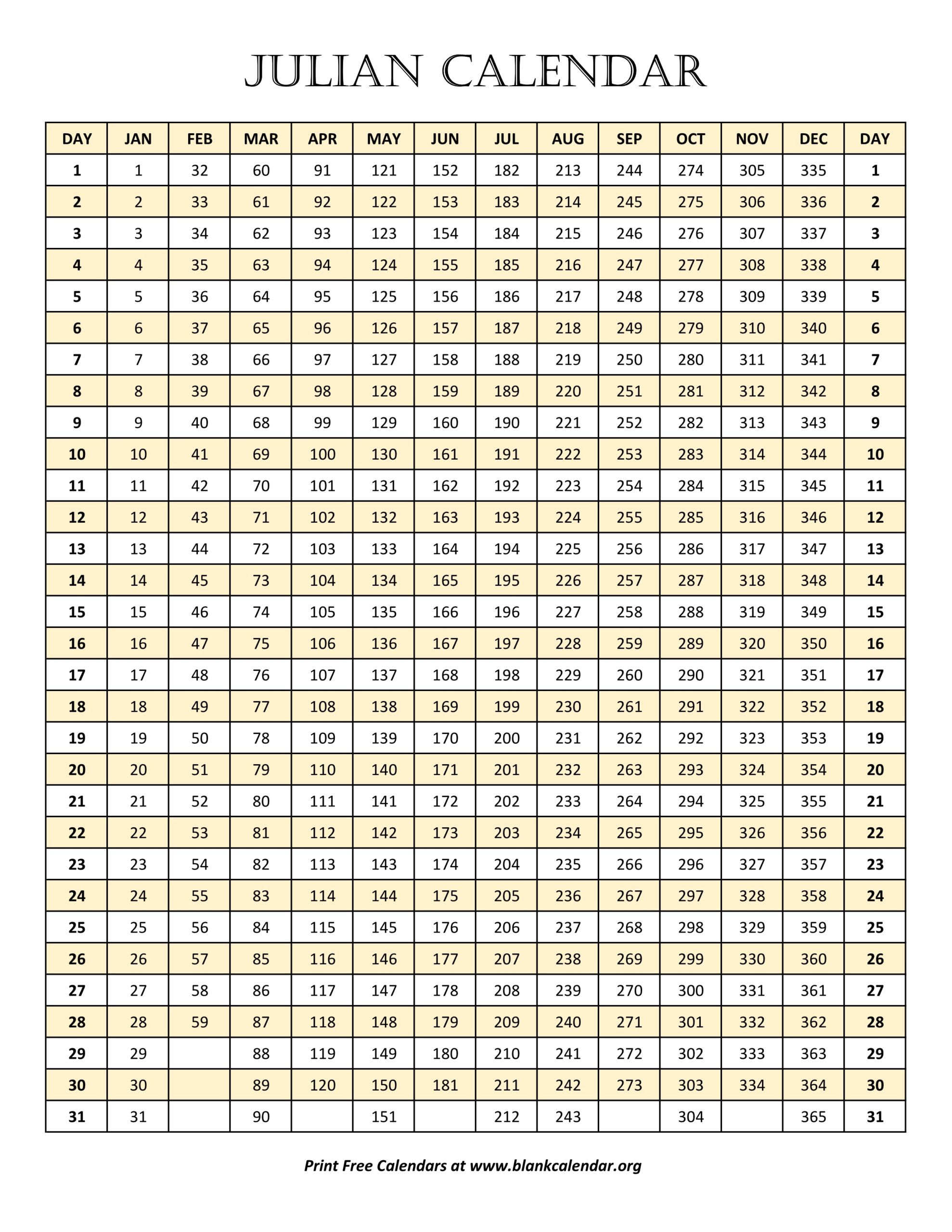
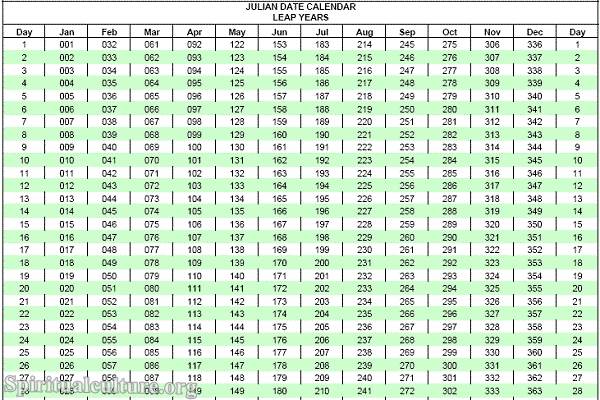
Closure

Thus, we hope this article has provided valuable insights into From Julian Dates to Calendar Dates: A Comprehensive Guide. We thank you for taking the time to read this article. See you in our next article!